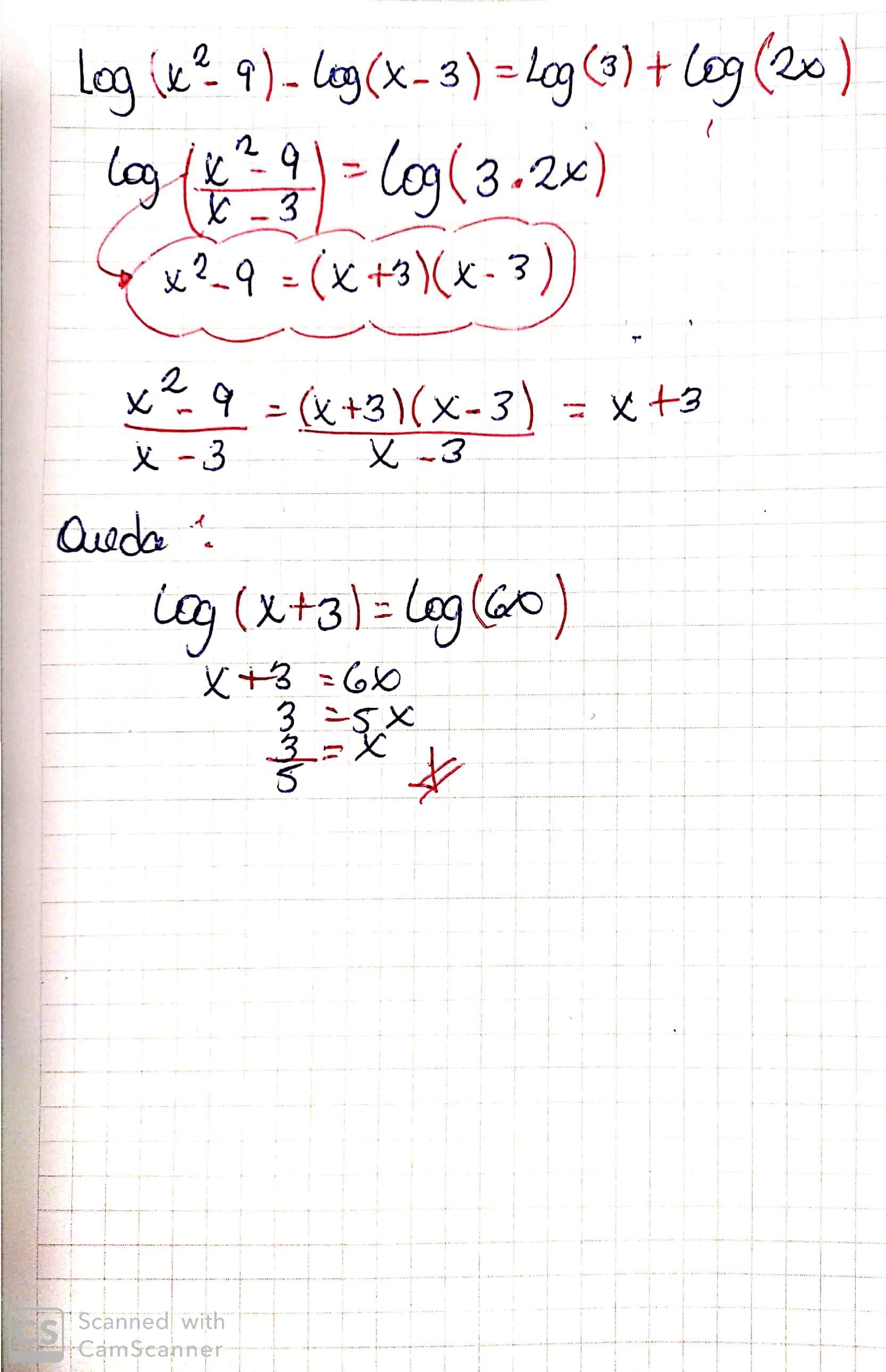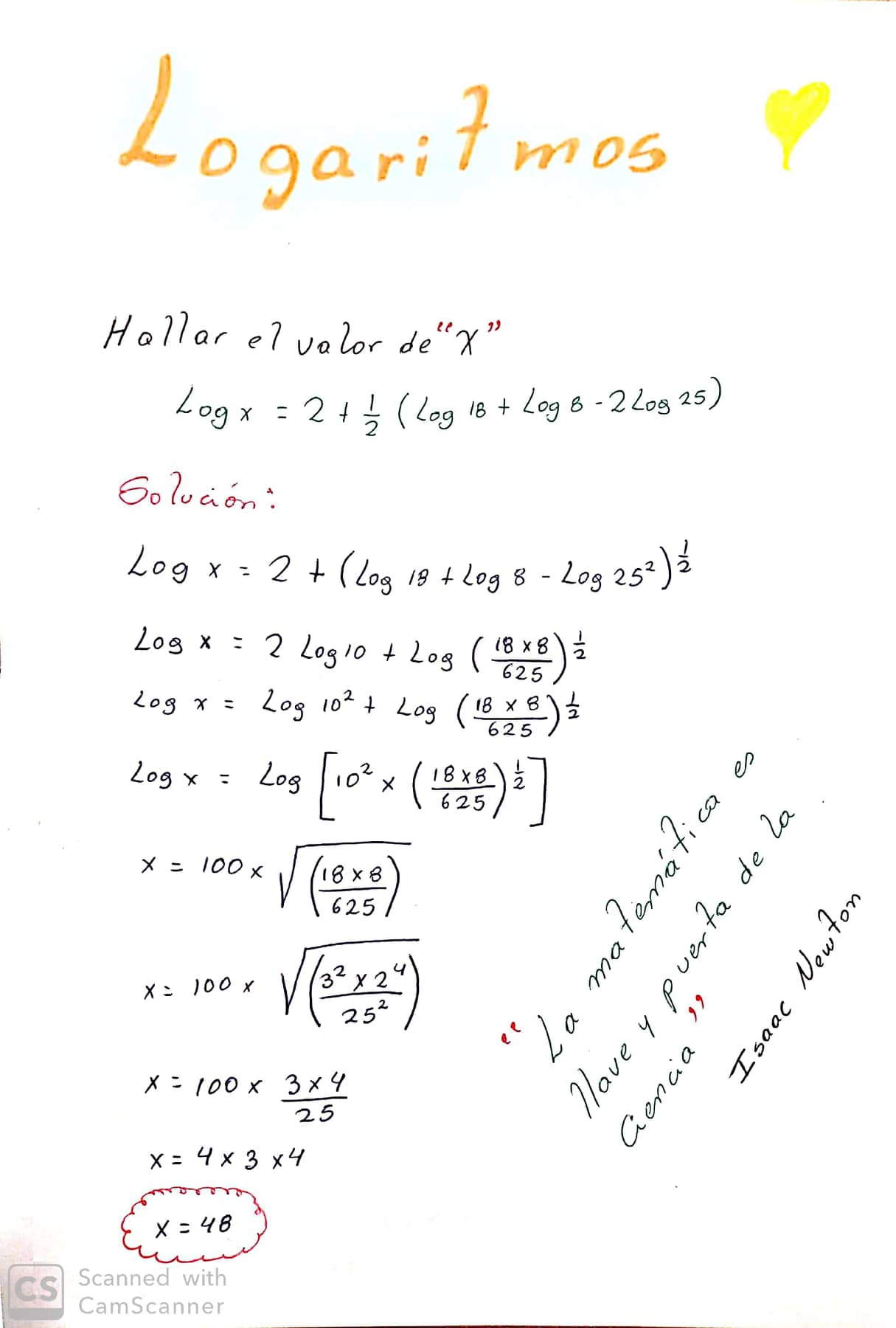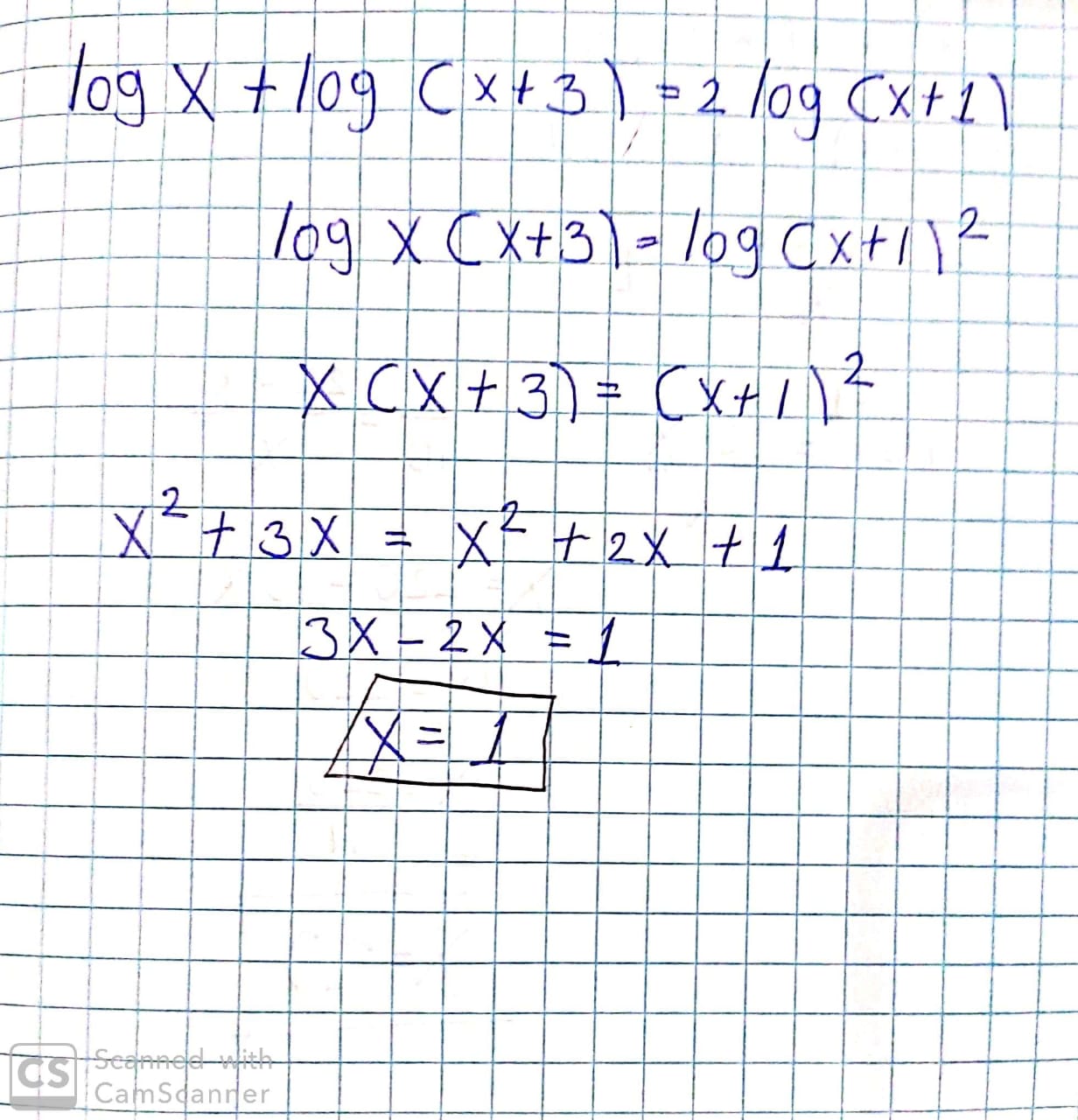
ECUACIONES LOGARITMICAS
La esencia de las matemáticas no es hacer las cosas simples complicadas, sino hacer las cosas complicadas simples
Acerca de mí
- El blog de Ecuaciones Logarítmicas es la agrupación de cuatro estudiantes de Matemáticas del I ciclo de la universidad, que al notar la dificultad para resolver los problemas decidieron juntarse y para brindar y compartir las soluciones de la mano con las formulas para su resolución. Todo comenzó en el aula y se convirtió en un proyecto que semana a semana subirá vídeos y ejercicios para conocimiento del público, principalmente para estudiantes universitarios.
OBJETIVO
- El blog tiene como objetivo enseñar las ecuaciones logarítmicas de manera didáctica, entregando recursos de buenas fuentes como vídeos y ejercicios resueltos, para su máximo desempeño en futuras tareas y ejercicios del tema. Pretendemos acompañarlos y guiarlos.
MISIÓN
- Ofrecer un espacio virtual a los jóvenes promoviendo la construcción de sus propios conocimientos a través del acompañamiento con videos explicativos para desarrollar logaritmos matemáticos de forma clara, precisa, confiable y adecuada mejorando su aprendizaje con un buen entendimiento del tema para un mejor aprovechamiento de estancia exacta.

VISIÓN
- Ser un equipo virtual para la difusión y mejor entendimiento de logaritmos matemáticos, en este blog los jóvenes encontraron una base y guía para el mejor desarrollo de competencias con ello elevar su calidad educativa y sus conocimientos.


propiedades logarítmicas
Propiedades
Logaritmo de la unidad
El logaritmo de 1 en cualquier base es igual a 0.
logb (1) = 0 ; con b ≠ 1.
Ej: log5 (1) = 0 porque 50 =1
log7 (1) = 0 porque 70 = 1
log20 1 = 0 ⇔ 200 = 1
Logaritmos de la base
El logaritmo de la base es igual a 1.
logb (b) = 1 ; con b ≠ 1.
Ej:
log5 (5) = 1 ⇔ 51 = 5
log6 (6) = 1 ⇔ 61 = 6
log12 (12) = 1 ⇔ 121 = 12
Logaritmo de una potencia con igual base:
El logaritmo de una potencia de un número es igual al producto entre el exponente de la potencia y el logaritmo del número.
logb bn = n, con b ≠ 1
Ej:
log6 6 3 = 3
Logaritmo de un producto
El logaritmo de un producto es igual a la suma de los logaritmos de los factores.
logb (a • c) = logb a + logb c
Ej:
logb (5 • 2) = logb 5 + logb 2
Logaritmos de un cociente
El logaritmo de un cociente es igual al logaritmo del dividendo, menos el logaritmo del divisor.
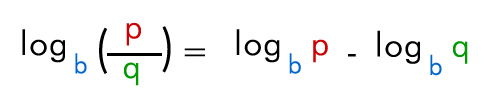
Ej:
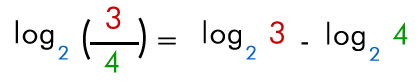
Logaritmo de una potencia
El logaritmo de una potencia es igual al exponente multiplicado por el logaritmo de la base.
loga cn = n loga c
Ej:
log3 10 2 = 2 log3 10
Logaritmo de una raíz
El logaritmo de una raíz es igual al logaritmo de la cantidad subradical dividido entre el índice de la raíz.
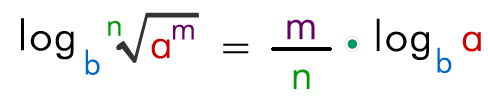
Ej:
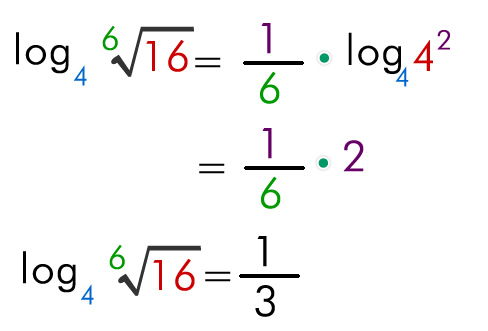
Cambio de base
 para todo p, a, b > 0; b, c ≠ 1
para todo p, a, b > 0; b, c ≠ 1
Ej:
log2 5 = log 5 / log 2